The Collapsed Wavefunction: Negative temperature?

Temperature in science is measured in Kelvins (K). 0 degrees Celsius is 273 K. Absolute zero is 0 K (-273 degrees C). Today's issue of Science has an article entitled "Negative absolute temperature of motional degrees of freedom". In this article, Braun et al. describe a system of potassium ions that have negative temperature. As you would expect, there are plenty of weird things that happen to a system with negative temperature.

Now, before I continue on any further, I need to make something clear. Negative temperature is not below absolute zero. After all, how can something be colder than absolute zero? The truth may sound even stranger - negative temperature is actually on the scale of temperatures after infinity. So the scale of temperatures is:

+0 K, . . . , +300 K, . . . , +∞ K, −∞ K, . . . , −300 K, . . . , −0 K

I can't stress enough, though, that we're really not talking about temperature here in terms of "hot" and "cold". We're talking about the entropy definition of temperature. The mathematical description of temperature is:

That is, the inverse of the temperature (T) is equal to the change in entropy (S) with respect to the change in energy (E). Negative temperature, then, means that as energy increases the entropy decreases. To anyone with an understanding of thermodynamics that might sound a little strange, and it is.

Wolfgang Ketterle, a physicist and Nobel laureate at the Massachusetts Institute of Technology in Cambridge, has said of this work: It is "as though you can stand a pyramid on its head and not worry about it toppling over" - what exactly does that mean? To understand it, lets look at some energy level diagrams.

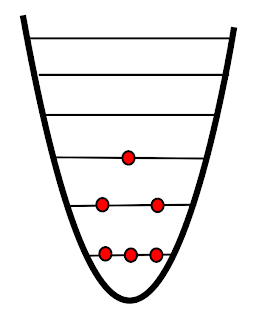
"Normal" temperature

The above diagram shows the quantum energy levels for some "normal" system. You'll notice that three of the particles are in the lowest energy level. As particles gain energy they are excited to higher levels. There are two in the first excited state, and one in the second excited state. If we describe entropy as the dispersal of energy you can see that as particles gain energy and are excited to higher levels the entropy increases - the particles are more "spread out".¹

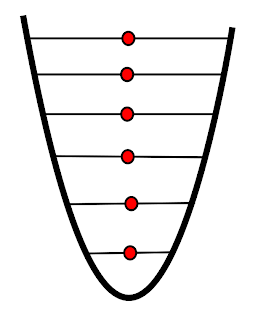
Infinitely high temperature

As temperature increases and the particles gain more and more energy they occupy more energy levels. Entropy will reach a maximum when the temperature is infinitely high.

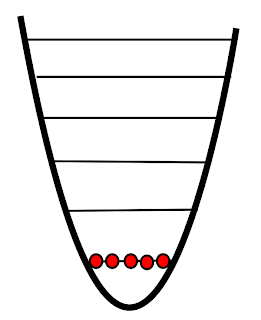
Absolute zero

On the other end of the temperature spectrum is absolute zero. At absolute zero all of the particles occupy the ground state energy level. A common misunderstanding of absolute zero is that at absolute zero motion ceases. Absolute zero does not mean that the atoms have no energy. Notice in the diagram for absolute zero that each particle is not at the bottom of the energy well. At absolute zero each particle will still have zero-point energy - the energy of the lowest quantum energy level. There can never be a state where the energy of a particle is zero. With no energy there would be no particle.

Negative temperature

Now on to negative temperature. This diagram looks similar to the one for "normal" temperature. You may notice, though, that there are more particles in the higher energy levels. This is not how things "should" work. Particles fill energy levels in a Boltzmann distribution - basically that means they will fill the lower energy levels more than the higher energy levels. You can see now why I quoted Wolfgang Ketterle earlier - the energy levels are filling like a pyramid on its top. This brings us back to the "spread out" definition of entropy. This temperature is negative because as energy is added to the system the particles are spread out into fewer energy levels, not more. They are forced to bunch up at the higher energy levels.

So how was this negative temperature reached? Well, to create a negative temperature you need to have an upper and lower bound to energy. Absolute zero is a lower bound to energy. You can't have a system with lower energy than absolute zero. The researchers needed an upper bound. But of course for a system near absolute zero there is nothing to stop energy from increasing - there's nowhere to go but up! Instead, they created an upper bound on energy by creating a optical lattice. Lasers arranged the potassium ions in such a way that there is an energetic barrier to the higher energy states. Thus, when energy is added to the system you get the inverted pyramid.

There are already plenty of ideas for applications of negative temperature. New quantum devices, heat engines with greater than 100% efficiency (without breaking the laws of thermodynamics), and even an explanation of dark matter. I don't see any of these as being realistic in the near future, though. What we gain from this right now is a better understanding of what temperature really is.

Notes

[1] I fully realize that this is not a rigorous definition of entropy, but it is useful definition. I'll be using it to explain negative temperature in a way that is hopefully helpful (and not too incorrect. Remember - all models are incorrect, some are just more useful than others)

If you enjoyed this article like us on or follow on .

Thursday, January 3, 2013

Negative temperature?